On obtient une onde périodique lors de la propagation d'une vibration. Afin d'expliquer ce qu'est une vibration, nous aurons recours au modèle traditionnel du ressort. Il nous permettra d'introduire les propriétés fondamentales des ondes périodiques, à savoir l'amplitude, la fréquence et la période, dans le cas particulièrement simple d'une onde périodique sinusoïdale.
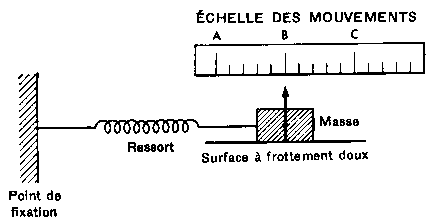
Figure 1 : Le modèle « masse-ressort »
Le ressort est relié à une masse. Ce système masse-ressort a une position de repos située au point B. (C'est-à-dire que, sans apport externe d'énergie, aucun mouvement ne sera jamais effectué : le ressort conservera sa tension et la masse demeurera au point B.)
Maintenant, si l'on pousse la masse vers le point A et qu'on la relache, la force exercée par le ressort aura tendance à la ramener au point B (la position de repos du système). Mais, en raison de la vitesse ainsi acquise - et d'un phénomène qu'on appelle l'inertie - la masse dépassera le point B pour foncer vers le point C.
Or, lorsque la masse atteint le point C, le même phénomène se produit : la force du ressort aura tendance à ramener la masse vers le point B ; et, à nouveau, le point B sera dépassé et la masse poursuivra sa course vers le point A, jusqu'à ce que, à nouveau, la force du ressort l'expulse dans l'autre direction.
Ces oscillations se poursuivront quelques temps, mais avec de moins en moins d'amplitude, jusqu'à ce que le système se stabilise à nouveau au point B. Ce phénomène est appelé amortissement du système. (Si notre système n'était pas amorti, les oscillations se poursuivraient indéfiniment, ce qui n'est possible qu'en théorie).
C'est ce mouvement d'un corps de part et d'autre d'un point de repos que l'on appelle une oscillation ou vibration.
En fait la vibration est facilitée par deux propriétés du système évoqué ci-dessus : la masse de l'objet déplacé (cause de l'inertie du système) et l'élasticité du ressort.
Pour la propagation des ondes sonores dans l'air, les molécules constituent des masses (même si celles-ci sont infimes, elles n'en ont pas moins une masse) et les forces reliant ses molécules se comportent comme un ressort.
Nous allons maintenant examiner les différentes caractéristiques permettant de définir ces oscillations.